
Carlos
Calvimontes Rojas*
|
|
No hay estudio del hombre que merezca
llamarse ciencia si no se basa en la demostración y argumentación
matemática.
Que nadie se atreva a adentrarse en los
fundamentos de mi obra si no es matemático.
Leonardo da Vinci (1452 – 1519)
|
|
There
is no study of the man that deserves to be called science when it is not
based on the mathematical demonstration and argumentation.
That
nobody dares to study in dept the basic principles of my work if he is
not a mathematician.
Leonardo
da Vinci (1452 – 1519) |
|
LEONARDO DA VINCI SE INSPIRO EN LA OBRA DE
VITRUVIO PARA SEÑALAR LAS PROPORCIONES HUMANAS; PERO ADEMAS
OCULTO EN ESA GEOMETRIA OTRA QUE, AL SER DECODIFICADA, DEMUESTRA
LA CONSTRUCCION DE UN CIRCULO DE IGUAL AREA QUE EL CUADRADO
DIBUJADO. CON ESA BASE SE RESOLVIO EL ANTIGUO PROBLEMA DE LA
‘CUADRATURA DEL CIRCULO’, SEGUN SU POSTULADO ORIGINAL: ‘A
PARTIR DE UN CIRCULO CONSTRUIR UN CUADRADO QUE TENGA LA MISMA
SUPERFICIE, SOLO CON EL EMPLEO DE UN COMPAS Y UNA REGLA SIN
GRADUAR'. |
|
LEONARDO
DA VINCI INSPIRED HIMSELF IN THE WORK OF VITRUVIO FOR INDICATING THE
HUMAN PROPORTIONS; BUT MOREOVER HIDDEN IN THAT GEOMETRY ANOTHER ONE THAT,
WHEN BEING DECODED, SHOWS THE CONSTRUCTION OF A CIRCLE OF EQUAL AREA
THAN THE SQUARE DRAWN. WITH THAT BASIS THE ANCIENT PROBLEM OF THE 'QUADRATURE
OF THE CIRCLE', ACCORDING TO ORIGINAL POSTULATE: 'ON BASIS OF A CIRCLE CONSTRUCT A SQUARE THAT HAS THE SAME
AREA, ONLY WITH THE USE OF A COMPASS AND A RULER WITHOUT GRADUATION' WAS
RESOLVED. |
|
*Con la colaboración de María
José Calvimontes C. y de Alfredo Calvimontes C.
*With
the cooperation of Maria José Calvimontes C. and of Alfredo Calvimontes
C. |
LEONARDO
Y VITRUVIO
El conocido esquema de Leonardo que muestra las
proporciones humanas se relaciona con el postulado que, quince siglos
antes, hizo sobre esa materia el arquitecto romano Marcus Vitruvius
Pollio en su obra De architectura. Leonardo mostró el
vínculo bajo el número 340 de su libro Tratado de Pintura [1] que,
poniendo entre paréntesis los criterios que no se encuentran en la obra
precedente, en forma escueta dice en la parte que interesa:
Según Vitruvio....... Si abres tanto las piernas
(que tu altura mengüe en 1/14,) y tanto extiendes y alzas los brazos
que con los dedos medios alcances la línea que delimita el extremo
superior de la cabeza, has de saber que el centro de los miembros
extendidos será el ombligo (y que el espacio que comprenden las piernas
será un triángulo equilátero). La longitud de los brazos extendidos
de un hombre es igual a su altura.
|
|
LEONARDO
AND VITRUVIO
The known scheme of Leonardo that
shows the human proportions relates with the postulate that, fifteen
centuries before, the Roman architect Marcus Vitruvius Pollio made on
this matter in his work De architectura. Leonardo has shown the link
under the number 340 in his book Treaty of Painting [1] that, putting
into parenthesis the criteria that are not found on the preceding work,
in concise form says in the part that is of interest:
According to Vitruvio..... When you open so much the
legs (so that your height decreases by 1/14), and extend and raise the
arms so that with the middle fingers you reach the line that limits the
upper end of the head, you have to know that the center of the extended
members will be the navel (and that the space that comprise the legs
will be an equilateral triangle). The length of the extended arms of a
man is equal to his height.
|
|
Vitruvio, según la traducción al castellano de
Angeles Cardona [3] -que
en esencia no difiere de otras-,
en forma extensa expuso:
El ombligo es el punto
central natural del cuerpo humano. En efecto, si se coloca un
hombre boca arriba, con sus manos y sus pies estirados, situando
el centro del compás en el ombligo y trazando una circunferencia,
ésta tocaría la punta de ambas manos y los dedos de los pies. La
figura circular trazada sobre el cuerpo humano nos posibilita el
lograr también un cuadrado; si se mide desde la planta de los
pies hasta la coronilla, la medida resultante será la misma que
la que se da entre las puntas de los dedos con los brazos
extendidos; exactamente
su anchura mide lo mismo que su altura, como los cuadrados que
trazamos con la escuadra.
|
|
Vituvio, according to the
translation into Spanish by Angeles Cardona [3] -that essentially does
not differ from others-, in an extended fashion explained:
The navel is the central point of
the human body. In fact, if a man is placed face up, with his hands and
feet stretched, placing the center of the compass at the navel and
drawing a circumference, this will touch the tip of both hands and the
fingers of the feet. The circular figure drawn on the human body enables
us to also achieve a square: if we measure from the sole of the feet up
to the crown of the head, the resulting measure will be the same than
the one between the tips of the finger with the extended arms; its width
measures exactly the same as its height, such as the squares we draw
with the set square. |
ANTECEDENTES
Y ENTORNO
A partir del descubrimiento en 1414 (sin sus
ilustraciones por habérselas perdido) de una copia manuscrita del libro
de Vitruvio, con los principios de la arquitectura clásica el interés
por el pasado, de artistas, arquitectos y mecenas, motivó que la labor
de hacer inteligible a esa obra recayera primeramente en eruditos
humanistas, arqueólogos, anticuarios, filólogos y gramáticos, dando
origen a una variedad de tratados [5], desde la obra de Alberti que
recuerda a Vitruvio, y a numerosas ediciones del libro de éste, una en
el siglo XV y por lo menos once en el XVI.
Asumiendo que Leonardo realizó
su dibujo entre 1485 y 1490, aparte de haber podido conocer manuscritos
de la obra de Vitrubio, la única edición de ella en su época que pudo
haber tomado en cuenta sería la que se supone se imprimió en Roma
entre 1486 y 1492, que empieza con una nota del editor, Iohannes
Sulpitius di Veroli, y se considera la edición príncipe de la obra.
Sulpitius usó los manuscritos más conocidos, pero dejó espacios en
blanco para los términos griegos, los epigramas y las ilustraciones; de
éstas sólo intentó una, un círculo.
También Leonardo pudo considerar la obra de Alberti
De re aedificatoria impresa en 1485; pero es posible que anteriormente
la haya tenido a su alcance, porque habían pasado más de treinta años
desde su presentación. Por otra parte, es evidente que leyó los
tratados que Francesco di Giorgio Martini hizo sobre la base de la obra
de Vitruvio. Con lo cual Leonardo habría tenido, aparte del
conocimiento de manuscritos de ésta, por lo menos tres referencias
sobre la misma y, sabiendo tanto de anatomía humana, pudo interpretar hábilmente
el criterio del arquitecto clásico.
Aunque la edición de Fra Giovanni Giocondo, impresa
en Venecia en 1511, fue realizada cuando aún vivía Leonardo y éste
pudo haberla conocido, ya no habría influido en su dibujo de las
proporciones de la figura humana. Fra Giocondo fue el primero en hacer
una edición crítica de la obra de Vitruvio, empleó material de
diferente procedencia, no dejó lagunas, reconstruyó las partes
griegas, produjo más de 136 ilustraciones, elaboró un glosario y una
tabla matemática para comprender el texto. El éxito de esa edición
determinó su reimpresión en 1513, 1522 y 1523.
El texto y las ilustraciones de
Fra Giocondo influyeron en las ediciones de De Architectura en el siglo
XVI. Sin embargo, pese a que el dibujo de Leonardo fue conocido y
utilizado por artistas y estudiosos desde esa época, hasta donde se
conoce no fue tomado en cuenta en ediciones posteriores ilustradas, que
no tienen la correcta interpretación que él hizo del postulado de
Vitruvio sobre las proporciones humanas. Actualmente, las más antiguas
y conocidas de esas ilustraciones son las de Francesco di Giorgio
Martini y Cesare di Lorenzo Cesariano.
Se puede entender que, en los
siglos en los que hubo mayor interés práctico por la obra de Vitruvio,
los editores hubiesen pretendido unidad y originalidad en la recreación
de las ilustraciones que se habían perdido; pero no se utilizó el
dibujo de Leonardo en ediciones tan tardías como la de Perrault que,
casi dos siglos después, ensayó una solución insatisfactoria de lo
que ya estaba resuelto, al mantener la misma distancia entre las líneas
horizontales que corresponden a la coronilla y a los pies, sin tomar en
cuenta que la estatura disminuye si se abre las piernas. |
|
BACKGROUND
AND SURROUNDINGS
From the discovery in 1414 on (without its
illustrations due to having lost them) of a handwritten copy of the book
of Vituvio, with the principles of the classic architecture the interest
for the past, of artists, architects and maecenas, motivated that the
task of making intelligible that work firstly fall on scholars,
humanists, archaeologists, antiquarians, philologists and grammarians,
giving origin to a variety of treaties [5], from the work of Alberti
that remembers Vituvio, and to numerous editions of the book of the
latter, one on the XV century and at least eleven on the XVI century.
Assuming that Leonardo made his drawing between 1485
and 1490, besides of having been able to know manuscripts of the work of
Vitruvio, the only edition of which in its time that could have been
taken into account would be the one that is supposed to be printed in
Rome between 1486 and 1492, that begins with a note of the editor,
Iohannes Sulpitus di Veroli and is considered the first edition of the
work, Sulpitus used the most known manuscripts, but left blank spaces
for the Greek terms, the epigrams and the illustrations; of these he
only tried one, a circle.
Also Leonardo could consider the work of Alberti De re
aedificatoria printed on 1485; but it is possible that he previously had
it available, because more than thirty years elapsed since its
presentation. On the other hand, it is evident that he read the treatise
Francisco di Giorgio Martini made on basis of the work of Vitruvio. With
which Leonardo has had, besides the knowledge of manuscripts, at least
three references about it and, knowing so much of human anatomy, could
skillfully interpret the criterion of the classic architect.
Although the edition of Fra Giovanni Giocondo, printed
in Venice on 1511, was done when Leonardo still lived and could have
known it, he no longer could have influenced on the drawing of the
proportions of the human figure. Fra Giocondo was the first in doing a
critical edition of Vitruvio's work, he employed material of different
origin, did not leave gaps, reconstructed the Greek parts, produced more
than 136 illustrations, prepared a glossary and a mathematical table for
understanding the text. The success of this edition determined its
reprint on 1513, 1522 and 1523.
The text and illustrations of Fra Giocondo influenced on
the editions of De Architectura on the XVI century. However, though the
drawing of Leonardo was known and used by artists and scholars since
that time, as far as it is known has not been taken into account in
subsequent illustrated editions, that lack the correct interpretation he
made of the postulate of Vitruvio about the human proportions. At
present, the oldest and most known of these illustrations are those of
Francesco di Giorgio and Cesare di Lorenzo Cesariano.
It can be understood that, on
the centuries where higher practical interest existed for the work of
Vitruvio, the editors had pretended unity and originality in the re-creation
of the illustrations that had been lost; but the drawing of Leonardo was
not used in editions so late as the Perrault's that, almost after two
centuries, tried an unsatisfactory solution of what had already been
solved, keeping the same distance between the horizontal lines that
correspond to the crown of he head and the legs, without considering
that the height decreases if the legs are opened. |
GEOMETRIA
MANIFIESTA Y OCULTA
Hasta la actualidad se
ilustra ediciones de De architectura con antiguos dibujos pero no
con el de Leonardo, que interpretó a Vitruvio, aunque con la
incorporación del valor de p
como diámetro del círculo y los
definidos por la Sección Aurea localizada en el ombligo; separación
entre el valor del Numero de Oro, F, y el de 1 en la estatura de
la figura humana. Estas modificaciones, señaladas claramente en
el esquema de Leonardo, determinan la diferencia entre el valor de
F y el de
p/2, (0,04723....), que equivale a un 1,8 % de la
estatura del hombre representado.
De lo que
no escribió Vitruvio: la disminución en 1/14 de la estatura de
la figura es una innovación de Leonardo. Aunque siempre se ha
pensado que tomando como centro el ombligo se forma un triángulo
isósceles en vez de uno equilátero, sin éste no se lograría la
fracción establecida por él. Se dice que Vitruvio no escribió
algo relativo a que ‘con los dedos de las manos se alcanza la
línea que delimita el extremo superior de la cabeza’; pero, al
referirse al cuadrado implicaría que los brazos extendidos, tanto
hacia arriba como lateralmente, alcanzan a los lados del cuadrado.
Leonardo dejó
deliberadamente, en su dibujo y escritos, cinco claves que se tomó
en cuenta en la decodificación de su esquema: la ubicación del
punto que define la Sección Aurea en el ombligo, la diferente
localización del centro del círculo y el diámetro de éste
igual a p,
el valor de 1/14 en la disminución de la estatura y el
planteamiento de la formación de un triángulo equilátero. Con
esos datos, se pudo hallar la solución gráfica de la ‘cuadratura
del círculo’; con valores matemáticos concluyentes, para un
problema cuya solución se consideró imposible de lograr, durante
milenios, pero que Leonardo conoció y ocultó en forma críptica.
|
|
REVEALED
AND HIDDEN GEOMETRY
Up to now illustrations of De
archithecture with old drawings but not with the one of Leonardo, that
interpreted Vitruvio though with the incorporation of the value of p as
diameter of the circle and those defined by the Golden Section located
at the navel, separation between the value of the Golden Number, F, and
the value of 1 in the height of the human figure. These modifications,
clearly indicated in the scheme of Leonardo, determine the difference
between the value of F and of
p/2, (0.04723....), that is equivalent to
an 1.8 % of the height of the represented man.
From what Vitruvio did not write,
the decrease of 1/14 in the height of the figure is an innovation of
Leonardo. Although it has always been thought that taking the navel as
center of the figure an isosceles triangle is formed instead of an
equilateral one, without this one the established fraction would not be
achieved. It is said that Vitruvio did not write something related to
that 'with the fingers of the hand the line that limits the upper end of
the head is obtained'; but, when referring to the square this would
imply that the arms extended, both upside and laterally, reach the sides
of the square.
Leonardo deliberately had left,
in his drawing and writings, five codes that were taken into account in
the decoding of his scheme: the location of the point that defines the
Golden Section in the navel, the different location of the center of the
circle and its diameter equal to p, the value of 1/14 in the decrease of
the height and the exposition of the formation of an equilateral
triangle. With this data, the graphic solution of the 'quadrature of the
circle' could be found, with conclusive mathematical values, for a
problem whose solution was considered as impossible to be achieved
during millenniums, but that Leonardo knew and hid in cryptic form. |
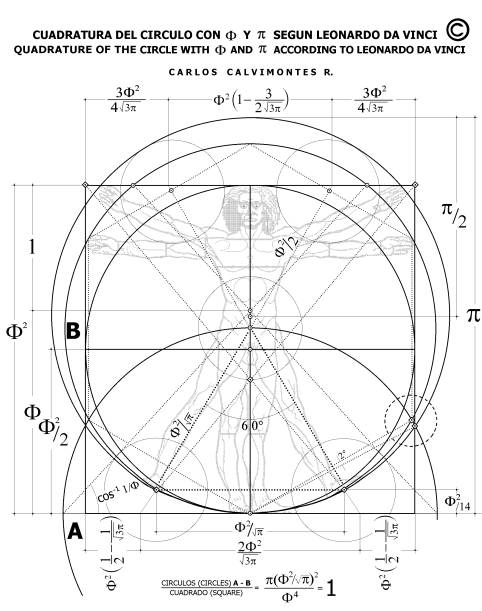
DEL
CUADRADO AL CIRCULO
Con centro en el punto medio
del lado inferior del cuadrado y como radio la distancia hasta el
extremo inferior de una de las cuerdas laterales del círculo con diámetro
p, se traza una circunferencia para conseguir el círculo A, con
área igual a la del cuadrado dado. Esa misma circunferencia, en su
intersección con el eje vertical del cuadrado, señala el centro del círculo
B que, tangente al lado inferior del cuadrado, obviamente tiene
igual superficie que éste. Con el centro del círculo como vértice
de un ángulo de 60°, que tiene por bisectriz al eje vertical, se forma
un triángulo equilátero que tiene de base la cuerda con flecha igual a
F2/14.
Con el procedimiento indicado se logra un círculo de igual área que la
de un cuadrado dado, con la intervención de F
y de p,
cumpliéndose además lo establecido por Leonardo.
Además, en el dibujo de
Leonardo, se observa que las líneas que unen los vértices inferiores
del triángulo equilátero con el punto localizado en el eje vertical, a
una distancia del centro del círculo dado igual a la cuarta parte de un
lado del exágono, en su proyección alcanzan los vértices superiores y
opuestos del cuadrado; y que la alineación de la recta que une la
intersección de la prolongación del lado inferior del cuadrado con la
circunferencia del círculo A, forma un ángulo igual a cos-1
de 1/F,
pasa por la Sección Aurea y confirma la ubicación de la intersección
de la circunferencia del círculo B con un lado del cuadrado.
Se debe tomar en cuenta que las
alineaciones, circunferencias, ángulos y tangencias, que se encontró
en el diseño de Leonardo, y se utilizó en la construcción para
encontrar puntos significativos de su decodificación, determinan la
coherencia geométrica de todo el conjunto y, además, tienen
correspondencia con partes definidas de la figura humana.
La solución específica que se
decodificó, para que a partir de un cuadrado con lado F2,
con la participación de un círculo con diámetro p,
se logre otro círculo con igual área que la de ese cuadrado, tiene
como clave que el radio que genera el círculo A, al rotar 2°
sobre el mismo centro, determina el radio del círculo B y un
lado del exágono regular inscrito en éste. La traslación del sistema
del círculo con diámetro p
y el cuadrado de lado F2,
a otro donde el cuadrado dado y el círculo oculto tienen áreas
iguales, constituye el artificio para esa solución. |
|
FROM
THE SQUARE TO THE CIRCLE
With center in the middle point
of the lower side of the square and as radius the distance to the lower
end of one of the lateral chords of the circle with diameter p, a
circumference is drawn for obtaining the circle A, with area
equal to that of the given square. That same circumference, in its
intersection with the vertical axis of the square, indicates the center
of the circle B that, tangent to the lower side of the square,
obviously has an area equal to such square. With the center of the
circle as vertex of an angle of 60°, that has as bisector to the
vertical axis, an equilateral triangle is formed having as basis the
chord with sagitta equal to F2/14.
With the indicated procedure a circle is achiever with area equal to the
given square, with the intervention of F
and of p,
complying further what was established by Leonardo.
Moreover, on the drawing of
Leonardo, it is noticed that the lines that put together the lower
vertexes of the equilateral triangle with the point located in the
vertical axis, at a distance from the center of the given circle equal
to the fourth part of one side of the hexagon, in their projection reach
the upper and opposed vertexes of the square, and that the alignment of
straight line that puts together the intersection of the prolongations
of the bottom side of the square with the circumference of the circle A,
forms an angle equal to cos-1 of 1/F,
passes by the Golden Section and confirms the location of the
intersection of the circumference of the circle B with one side
of the square.
It must be taken into account
that the alignments, circumferences, angles and tangencies found in the
drawing of Leonardo and used in the construction for finding significant
points of its decodification, determines the geometric coherence of all
the assembly and, moreover, has correspondence with defined parts of the
human figure.
The specific solution that has
been decoded, so that on basis of a square with side F2,
with the participation of a circle of diameter p,
other circle be obtained with equal area than that of that square, has
as key that the radius that generates the circle A, when rotates
2° on the same center, determines the radius of the circle B and
one side of the regular hexagon inscribed in it. The translation of the
system of the circle with diameter p
and the square of side F2,
to another one where the given square and the hidden circle have equal
areas, constituting the trick for this solution. |
|
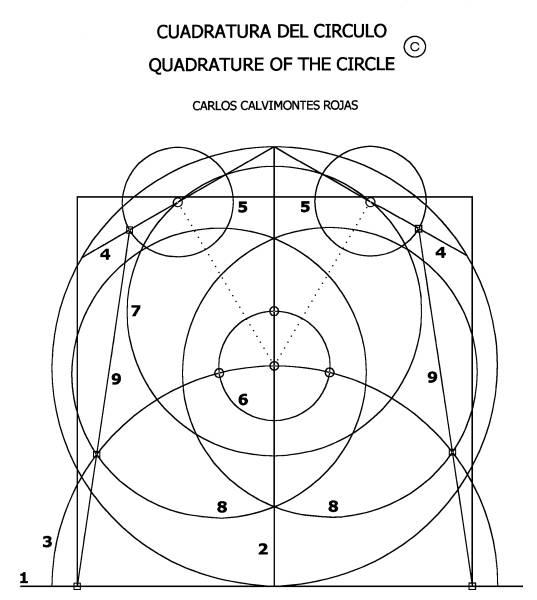
DEL
CIRCULO AL CUADRADO
Para atender al postulado
original del problema, que dice que partiendo de un círculo dado sólo
‘con compás y regla sin graduar’ se obtenga un cuadrado que tenga
la misma superficie, se hizo abstracción del círculo y del cuadrado
dibujados por Leonardo y se partió del círculo que él ocultó, con la
incorporación de: una línea tangente a ese círculo, una perpendicular
levantada en el punto de tangencia, dos lados del exágono inscrito
y de un arco circular con igual
radio que el del círculo dado con
centro en el mismo punto de tangencia.
Con un radio igual a la cuarta
parte de un lado del exágono se dibujó tres círculos auxiliares
iguales; dos de ellos con sus centros en la mitad de los lados dibujados
del exágono, en la parte opuesta a la tangente; y, con el mismo centro
del círculo dado, el tercero. Con centro en la intersección de éste
con la perpendicular, tomando como radio la distancia hasta la mitad de
las cuerdas, se hizo otro círculo. Con el radio anterior, con centros
en las intersecciones del arco circular con el mismo tercer círculo
auxiliar, se trazó otros dos círculos. Las intersecciones de éstos
con el arco circular señalan los puntos clave para definir la
‘cuadratura del círculo’.
En efecto, la línea que une
cada uno de dichos puntos con las intersecciones de los círculos
trazados sobre las cuerdas con éstas (en su parte más alejada de la
perpendicular), en su prolongación hasta la línea tangente definen
sobre ésta la longitud del lado del cuadrado de igual área que la del
círculo dado. |
|
FROM
THE CIRCLE TO THE SQUARE
For taking care of the original
postulate of the problem that states that starting from a given circle
only 'with compass and ruler without graduation' a square be obtained
having the same area, abstraction has been made from the circle and the
square drawn by Leonardo and it has been started from the circle
he did hide, with the incorporation of a line tangent to that
circle and a perpendicular lifted at the point of tangency, two sides of
the inscribed hexagon and a circular arch of same radius than the given
circle with center in the same point of tangency.
With a radious equal to the
fourth part of one side of the hexagon three auxiliary equal circles
were drawn; two of them with its centers at the middle of the drawn
sides of the hexagon, in the part opossed to the tangent; and, with the
same center of the given circle, the third one. With center in the
intersection of this with the perpendicular, taking as radious the
distance to the middle of the chords. another circle was made. With the
former radious, with center in the intersections of the circular arch
with the same third auxiliary circle, another two circles were made. The
intersections of these with the circular arch indicate the key points
for defining the ‘quadrature of the circle’.
Indeed, the line that joins each
one of such points with the intersection of the circles drawn on with
these (on its part that are more away from the perpendicular), in its
prolongation up to the tangent line defines about this the length the
side of the square of the same area than that of the given circle. |
|
 |
BIBLIOGRAFIA
BIBLIOGRAPHY
1.
DA VINCI, LEONARDO. Tratado de la
Pintura. Edición preparada por Angel González García. Editorial
Nacional. Madrid, 1980.
2.
DA VINCI, LEONARDO. Tratado de la
Pintura. Traducción al castellano sobre el original francés de André
Keller por Angeles Cardona. Reimpresión íntegra de la edición
italiana de Bolonia (1786), publicada en París por Rafael Trichet de
Fresne. Editora de los Amigos del Círculo del Bibliófilo. Barcelona,
1979.
3.
VITRUVIO POLLIO, MARCO. Los Diez
Libros de Arquitectura. Traducción al castellano por José Oliver
Domingo. Introducción de Delfín Rodríguez Ruiz, Alianza Editorial.
Madrid, 1995.
4.
VITRUVIO POLLIO, MARCO. Los Diez
Libros de Arquitectura. Traducción directa del latín al castellano, prólogo
y notas de Agustín Blánquez. Editorial Iberia S. A., Barcelona, 1991
5.
WIEBENSON, DORA. Los Tratados de
Arquitectura. Editorial Hermann Blume, Madrid, 1988. |
|
|
|
|
|
IR AL
ÍNDICE
http://urbtecto.es.tl
urbtecto@gmail.com |