Carlos Calvimontes Rojas

El 'domo exapenta' (o hexapenta) tiene una forma prácticamente semiesférica generada por la presencia armonizadora de pentágonos en conjuntos de exágonos (o hexágonos), que pueden estar respectivamente reticulados por triángulos isósceles y equiláteros. Esa forma, que responde con relevantes condiciones estéticas, constructivas y estructurales a la doble exigencia arquitectónica de encerrar y cubrir espacios, tiene su contraparte en otras existentes en la Naturaleza, representadas por el paradigma geométrico del icosaedro truncado de la molécula gigante del carbono 60 y por la extraordinaria belleza de los radiolarios.

Convencionalmente se denomina exapenta al icosaedro truncado y a otros poliedros formados por un mayor número de exágonos y pentágonos regulares, que se muestran en la Naturaleza y en la obra humana en sendas extensas variedades por la diferencia entre el número de esas dos figuras geométricas en cada cuerpo. Sin embargo, existe un patrón común en la configuración de todos esos poliedros, determinada por la consonancia existente entre exágonos y pentágonos que tienen la misma longitud de sus lados por ser éstos comunes entre ambas figuras: la relación de sus apotemas está definida por el Número de Oro.

EL NÚMERO DE ORO EN LA ARMONÍA DE LO CREADO

En un mismo campo fenoménico, dos cosas de la misma especie pero de diferente magnitud armonizan si entre ellas se manifiesta el Número de Oro (o su figura emblemática, el pentágono), módulo de la relación de consonancia en ese relativo desequilibrio característico de lo que tiene vida, la tuvo o tiende a ella, y de lo que ha tenido o tiene movimiento molecular, como en las estructuras dinámicas, en contraposición a la predominancia del exágono en lo inerte que tiene el equilibrio cristalino propio del mundo mineral.

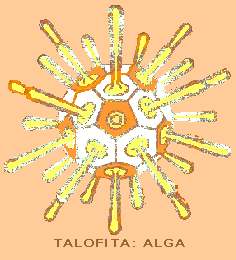Sin embargo, en la infinidad de formas geométricas existentes en las obras de la Naturaleza, no hay una polaridad entre aquellas cosas que muestran la presencia o traducen las proporciones de pentágonos y otras que están impregnadas por exágonos o sus derivaciones; hay unas terceras donde coexisten ambas figuras o sus proporciones, en manifestaciones de lo vivo y lo inerte, lo dinámico y lo estable, lo orgánico y lo inorgánico, lo que tiene mayor o menor entropía.

ARMONÍA EN LA ARQUITECTURA Y EN TODA CREACIÓN HUMANA

Entre renombrados arquitectos con el mismo pensamiento es ejemplar la figura de Antoni Gaudí, cuya obra tuvo como constante su inspiración en el "gran libro de la Naturaleza". Al establecer él que "la calidad esencial de la obra de arte es la armonía" explica que "la arquitectura crea el organismo y por eso éste debe tener una ley en consonancia con las de la Naturaleza", porque éstas no son otras que las de la armonía que el hombre reconoce y asume, para repetirlas en lo más excelso de su creación.

En general, como producto de acciones determinadas por la intuición o por la reflexión, el factor de coherencia para valorizar una obra arquitectónica por la armonía entre sus partes es el Número de Oro, que añade a su rol estético otro que condiciona medidas y proporciones por ser connatural al hombre. Por eso mismo, éste también utiliza patrones de composición y proporción, con los mismos principios físicos y geométricos de la armonía preestablecida, para valorizar su obra artística e utilitaria en diferentes campos.

EXAPENTAS EN LA NATURALEZA

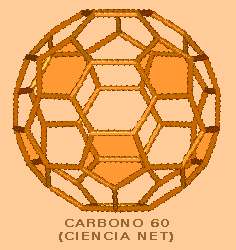
Aunque es propio de la química inorgánica, el carbono, a través de sus compuestos, genera toda la química orgánica. Además de esa excepcional peculiaridad, por la cristalización de sus moléculas tiene otras formas alotrópicas aparte de las del grafito (sistema cúbico) y del diamante (sistema exagonal). En ellas se destaca la molécula gigante, hueca y esférica del carbono 60, que en un icosaedro truncado reúne con máxima economía pentágonos y exágonos regulares.

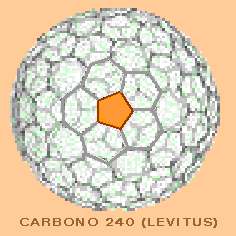La molécula del C60, abundante en el universo pero descubierta recién en 1985, tiene propiedades únicas (que no se acaba de descubrir) en la química y en la física, destacándose en su forma y estructura la simetría más alta existente entre todas las moléculas conocidas y la belleza de lo perfecto. Junto con su descubrimiento se hizo el de otras moléculas similares: C240 y C540. Éstas no por ser cada vez más grandes son progresivamente más esféricas ni tampoco aumentan su simetría; sino que conservan la del C60.

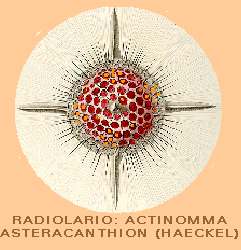
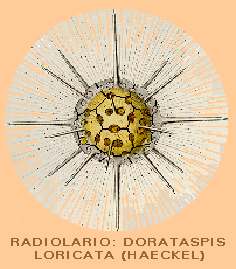
Entre lo mineral y lo que tiene vida, como en un juego de espejos, a los carbonos recién encontrados se les contraponen los radiolarios (protozoarios que hacen una de las más simples áreas de lo orgánico). Son minúsculos animales marinos unicelulares, con esqueleto de sílice, en su mayoría de forma esférica; de excepcional belleza por las combinaciones de pentágonos y exágonos en la gran variedad de las formas de sus perforaciones, complementadas con los seudópodos radiales que determinan su nombre.

También entre los protozoarios están los foraminíferos, de los cuales los más difundidos y abundantes se encuentran en el género de las globigerinas, que reciben este nombre por presentar su concha formada por varias cámaras globulosas constituidas por carbonato de calcio, las cuales permiten que el animal flote. Entre los varios cientos de especies de globigerinas que se conoce actualmente, existen unas que tienen el conjunto de sus cámaras con la armoniosa configuración de un exapenta regular.

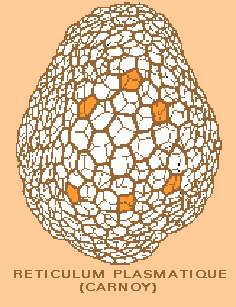
En los procesos físico-químicos de partición del espacio con el resultado conocido como espuma, el conjunto de las paredes de los compartimientos busca la mínima extensión posible de superficie, en una diversidad de soluciones en las que se debe cumplir condiciones de forma y relación. Con ese condicionamiento y la tendencia adicional de que el conjunto de burbujas busca la esfericidad, hay espuma formada por poliedros irregulares que tienen entre sus lados: cuadrados, pentágonos y exágonos.

EXAPENTAS EN LA OBRA HUMANA

Luca Paccioli (1445-1517), para su libro De Divina Proportione (1498) se inspiró en las obras de Arquímedes y de su maestro Piero della Francesca (1420-1492), pintor y matemático, e hizo de diversos poliedros modelos huecos de madera, que Leonardo da Vinci (1452-1519) utilizó para hacer las ilustraciones de ese libro. Al haberse encontrado en el siglo XX manuscritos de la obra de della Francesca, se comprobó la existencia del dibujo más antiguo conocido del icosaedro truncado.

Paccioli, importante exponente de la relación entre arte y matemáticas en el Renacimiento, aparte de contribuir al mejor conocimiento de los poliedros, se refirió a la amplia presencia del Número de Oro en la Naturaleza y, por esa razón, le adjudicó el nombre de Divina Proporción, como patrón de la armonía en todo lo creado. Aunque él no lo señaló, como demostración de esa armonía y confirmación de la designación que propuso, está también el icosaedro truncado que figura en su libro.

Buckminster Fuller, quien relacionó la Naturaleza con su obra, pudo haber conocido el estudio de Ernst Haeckel (Die Radiolarien, 1862) y el de D'Arcy Thompson (On Growth and Form, 1917), donde se muestra y analiza la configuración de los radiolarios, para fundamentar en la década de 1940 su exitoso impulso a la utilización de lo que él llamó el 'domo geodésico', originalmente creado por el ingeniero alemán Walter Bauersfeld en 1922 para instalar un planetario de la Zeiss en Jena.

En la historia del fútbol ha sido importante la preocupación por contar con una pelota que combine la mayor y constante esfericidad con la regularidad de la distribución de las costuras que son necesarias por las características del juego. Esa doble condición tuvo la respuesta perfecta en la simetría de la Telstar de 1970. Aunque se ha producido una gran evolución en el uso de materiales, no ha variado esa forma geométrica, ni su peso y tamaño, hasta llegar a la Fevernova del 2002.