GEOMETRY
IN
THE ANCIENT EGYPT
CARLOS CALVIMONTES ROJAS
STUDY CONTEXT
PLACE
 |
Excavated on the left side of the Valley of the Kings, among many others of
the Empire of New Egypt, is the tomb of Ramses IX (11th century BC). It is
the first one the visitor finds, after crossing the entrance door to the
place. There is the drawing of a human figure, a snake that forms a right
angle and a beetle in a set of rectangles.
|
ANTECEDENT
In the mid-twentieth century, R. A. Schwaller de Lubicz
found that this human figure is supported by the hypotenuse of a right triangle
3-4-5 whose catheti are shaped by
the snake. He also thought he had found the proportional values of
p
and
F related to the human figure but his calculations and
graphical demonstrations do not show satisfactory results.
CONTENT
The results presented below correspond to the analysis
of said drawing in its entirety. This one gathers a set of geometric solutions,
anthropometric proportions and the values of
p
and
F, in an ingenious lasting testimony of knowledge from a
far period and hidden as it was done in other representative designs of remote
cultures.
COMPOSITION
The drawing contains two sets: one is that of the
beetle and two rectangles; the other the one of the human figure and the
serpent. The two sets are independent, both in their design and in their
interpretation. To motivate this, some signs were left in the drawing that, due
to their position, dimension, proportion and geometry, could be singled out and,
in some cases, associated.
DECODING
From what has been observed in similar cases, in
testimonies of the knowledge of geometry in the remote cultures of Sumer and
Tiwanaku, by the presence of the numerous signals and patterns found especially
in the second set it was assumed that it encrypted several messages and that it
was necessary to discern signs and patterns that would serve to decipher each
one.
PROCESS
In the development of the study it was found
indications that although they were clear they were not for a single message,
showing that the same graphic had been used to hide different approaches. To
group the signs and discover different reading patterns for each message, we
looked for how to make alignments, draw geometric figures, size them and find
centers of circles, in a long iterative process going from the simplest to the
complex.
RESULTS OF
THE STUDY
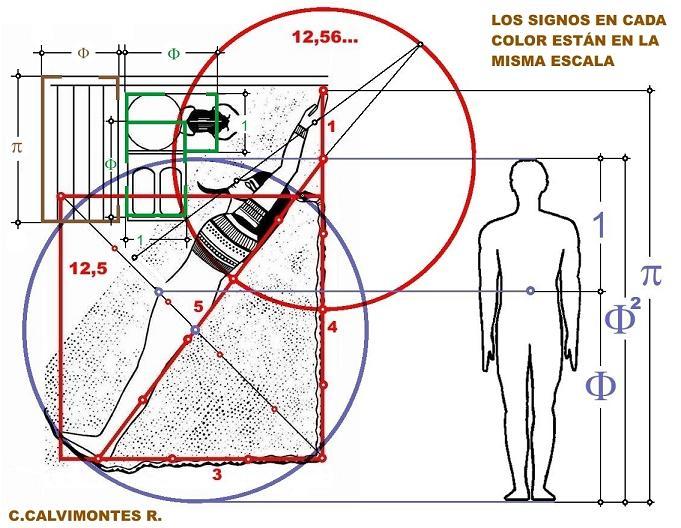
RECTANGLES
In the configuration of the beetle set two golden
rectangles are hidden because they have sides 1 and
F.
The other one, to the left, is divided significantly into 5 columns (the 5 is
essential for the knowledge of
F)
and has sides
p and
F.
TRIANGLE
The human figure (in the hypotenuse) with the serpent
(in the cathetus) make a right triangle 3-4-5. The extended arm, in the
extension of the catheti with value 4, makes another unit to show the way to
solve that type of triangles in that culture as it was done in Sumer 10
centuries before:
In right triangles whose sides are measured with
integers if: the hypotenuse is odd, one catheti is odd with the other pair and
the difference between the largest and the hypotenuse is 1 or 2; the value of
the hypotenuse is equal to the major catheti plus 2 if the minor catheti is even
and 1 if it is odd.
It is known that Pythagoras, six centuries later, spent
more than twenty years on study trips to Egypt, Mesopotamia (where Sumer was),
Byblos, Tire, Syria and India. It is very possible that he has known the drawing
in the tomb of Ramses and the Sumerian solution (recorded by Gudea in his most
famous sculpture). Later it would become famous by the solution of the right
triangle with the squares supported in its sides.
QUADRATURE
|
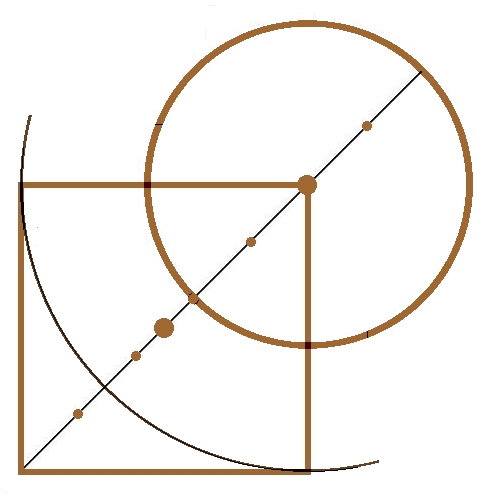 |
The signs of the right angles that the snake forms in
its neck and in its central part, the ends of the foot of the human figure
and the direction indicated by the beard, determine the configuration of a
square; and, the phallus shows the direction of the diagonal of that
geometric figure. With the same scale of the triangle and associated with
it, the square has a surface of 12.5 and its diagonal measures 5.
The prolongation of the hypotenuse crosses that of the
alignment defined by the end of the phallus, the tip of the nose and the
back of the hand. The distance between that intersection and that of the
hypotenuse and the catheti with value 4, is the radius of a circle with
surface 12.56 ...
The set of square and circle is a simple solution of
the 'quadrature of the circle', but with a discrepancy of 0.5%. It would
probably be the oldest known and proven, according to the approach:
From a circle, construct a square that has the same
surface, only with the use of a compass and an ungraded rule.
|
PROPORTIONS
Solution A
The intersection of the diagonal of the square with the
hypotenuse marks the center of a circle that has as a radius the distance to the
ends of the head and foot of the human figure. Assuming the turn of this one to
put its axis parallel to the cathetus
with value 4, considering that it is proper for man to have his height
equivalent to
F2
his navel indicates the golden section with the division of 1 and
F, aligned with the lower point of the base of the
phallus.
Being the diameter of the circle equivalent to
F2,
this plus the unit added to the cathetus with value 4, until the end of the
extended arm, determines the proportional value of
p.
The values of
p and
F
can be as they are now known, depending on the layout and size of the geometric
figures; however, the trigonometric analysis establishes a margin of discrepancy
of 1 per thousand; to give 3.14 instead of 3.1415 in the case of
p and 1.62 instead of 1.618 in the case of
F.
Solution B
With the same design used in the reading to find
Solution A, the circle is achieved. Likewise, the human figure is rotated to its
vertical position, but with a smaller stature, having as limits the upper part
of the circle and the base of the square; obviously that height is equivalent to
F2,
being the proportion of man; however, there is no signal to locate
F in the navel in relation to any signal in the human
figure.
With center in the vertex formed by the hypotenuse and
the catheus with value 4, and with a
radius with value 1 indicated by the extended arm in the direction of that
cathetus, a circular arc is traced until intercepting the prolongation of the
hypotenuse, being achieved in the vertical direction a dimension of 0.8 that
added to that of the same cathetus
gives 4.8 to proportionally show the value of
p.
By the trigonometric solution, or by the congruence of
triangles, it is determined that if the height of the man is 4 and equals
F2, the total length of 4.8 equals a p of 3.1416 ...,
with a difference less than 4 in one hundred thousand of the value known now.
This result could show that in that culture the ratio between 4.8 and 4 (equal
to 1.2) was known, as it was used in other cultures and epochs, to relate ap
with
F, by means of F2 that is the paradigm of the human
proportion.
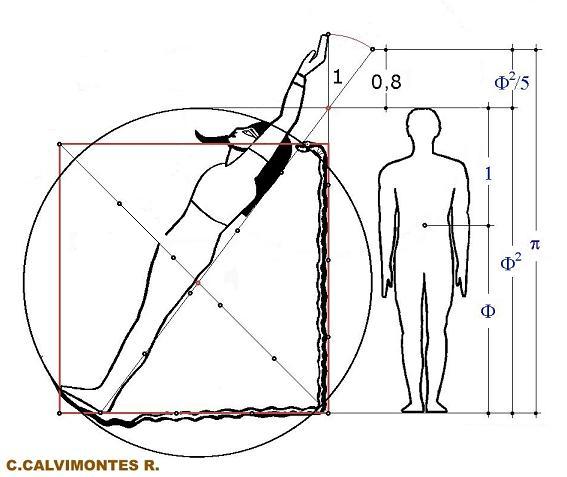
CONTRIBUTION OF S. DE LUBICZ
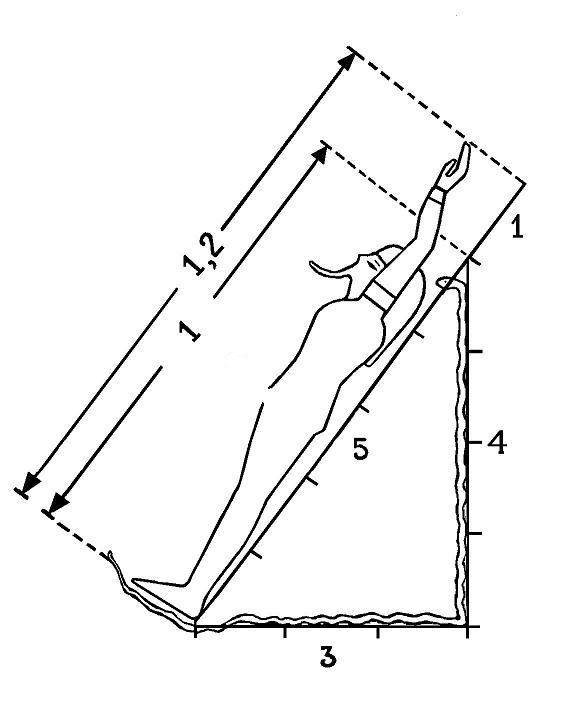
 |
In the book Secrets of the Great Pyramid, mention is
made of the discovery made by RA Schwaller de Lubicz of triangle 3-4-5 and
of the values of
p and
F
in the drawing found in the tomb of Ramses IX. He would have established
that the phallus divides the body into 1 and
F, giving a total of
F2.
The length of the hypotenuse, 5 or 1, is greater than
the height of the human figure represented, although the total height of the
figure with the raised arm is 6 or 1.2. However, although the ratio between
p and
F2 is approximately 1.2, it does not correspond to the
proportions indicated in the second drawing. Furthermore, according to the
anthropometric proportions, it is impossible for the phallus to divide the
human figure into 1 and
F.
That is, the first drawing only expresses the relation
of the length of the hypotenuse with the height indicated by the arm raised
by the character (5 and 6, or 1 and 1, 2), without taking into account the
height of the man. The second drawing shows
F2,
equating √5 + 3 with a value of 1; and, the length shown as 1.2
F2
equated with √5 + 4 has a proportional value of 3,118 ... which is far from
being that of
p.
Despite these errors, it is recognized that Schwaller
de Lubicz found triangle 3-4-5 and sensed the presence of
p and
F.
|
Books of the author:


GO TO THE MAIN PAGE
http://urbtecto.es.tl