GEOMETRÍA EN EL ANTIGUO EGIPTO
CARLOS CALVIMONTES ROJAS
CONTEXTO DEL ESTUDIO
LUGAR
 |
Excavada en el lado izquierdo del Valle de los Reyes,
entre muchas otras del Imperio del Nuevo Egipto, se encuentra la tumba de
Ramsés IX (siglo XI a.C.). Es la primera que encuentra el visitante, después
de cruzar la puerta de entrada al lugar. Ahí se encuentra el dibujo de una
figura humana, una serpiente que forma un ángulo recto y un escarabajo en un
conjunto de rectángulos.
|
ANTECEDENTE
A mediados del siglo
XX, R. A. Schwaller de Lubicz encontró que dicha figura humana está apoyada en
la hipotenusa de un triángulo rectángulo 3-4-5 cuyos catetos están configurados
por la serpiente. También creyó haber encontrado los valores proporcionales de
p y
F relacionados
con la figura humana pero sus cálculos y demostraciones gráficas no muestran
resultados satisfactorios.
CONTENIDO
Los resultados que se
presenta a continuación corresponden al análisis de dicho dibujo en su
integridad. Éste reúne un conjunto de soluciones geométricas, proporciones
antropométricas y los valores de
p y
F, en un
ingenioso testimonio perdurable de conocimientos de una remota época y oculto
como se hizo en otros diseños representativos de remotas culturas.
COMPOSICIÓN
El dibujo contiene dos
conjuntos: uno es el del escarabajo y dos rectángulos; el otro el de la figura
humana y la serpiente. Los dos conjuntos son independientes, tanto en su diseño
como en su interpretación. Para motivar ésta se dejó en el dibujo algunas
señales que, por su posición, dimensión, proporción y geometría, se pudiesen
singularizar y, en algunos casos, asociar.
DESCIFRAMIENTO
Por lo que se ha
observado en casos semejantes, en testimonios del conocimiento de la geometría
en las remotas culturas de Sumer y Tiwanaku, por la presencia de las numerosas
señales y pautas encontradas sobre todo en el segundo conjunto se asumió que
éste encriptaba varios mensajes y que era necesario discernir de señas y pautas
las que servirían para descifrar cada uno.
PROCESO
En el desarrollo del
estudio se fue encontrando indicios que si bien eran claros no eran para un solo
mensaje, haciendo ver que se había empleado el mismo grafico para ocultar
diferentes planteamientos. Para agrupar las señas y descubrir pautas de lectura
diferente para cada mensaje, se buscó cómo hacer alineaciones, dibujar figuras
geométricas, dimensionar éstas y encontrar centros de círculos, en un prolongado
proceso iterativo yendo de lo más simple a lo complejo.
RESULTADOS DEL ESTUDIO
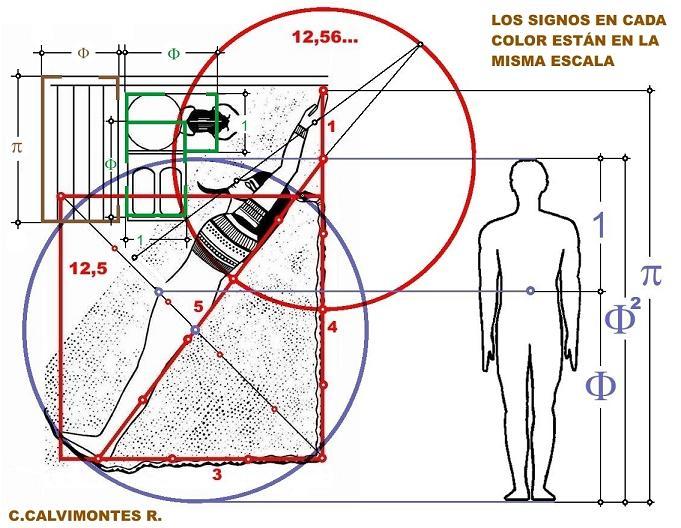
RECTÁNGULOS
En la configuración
del conjunto del escarabajo se ocultan dos rectángulos áureos pues tienen por lados 1 y
F. El
otro, a la izquierda, está dividido significativamente en 5 columnas (el 5 es esencial para el
conocimiento de
F)
y tiene por lados p y
F.
TRIÁNGULO
La figura humana
(en la hipotenusa) con
la serpiente (en los catetos) hacen un triángulo rectángulo 3-4-5. El brazo extendido, en la
prolongación del cateto con valor 4, hace otra unidad para mostrar la
forma de resolver ese tipo de triángulos en esa cultura como se lo hacía en Sumer 10 siglos antes:
En los triángulos rectángulos cuyos lados se miden con
números enteros si: la hipotenusa es impar, un cateto es impar siendo el otro
par y la diferencia entre el mayor y la hipotenusa es de 1 ó 2; el valor de la
hipotenusa es igual al cateto mayor más 2 si el cateto menor es par y más
1 si
es impar.
Es conocido que
Pitágoras, seis siglos más tarde, estuvo más de veinte años en viajes de estudio en
Egipto, Mesopotamia (donde estuvo Sumer), Biblos, Tiro, Siria e India. Es
muy posible que haya conocido el dibujo en la tumba de Ramsés y la solución
sumeria (registrada por Gudea en su escultura más conocida). Después se haría
famoso por la solución del triángulo rectángulo con los cuadrados apoyados en
sus lados.
CUADRATURA
|
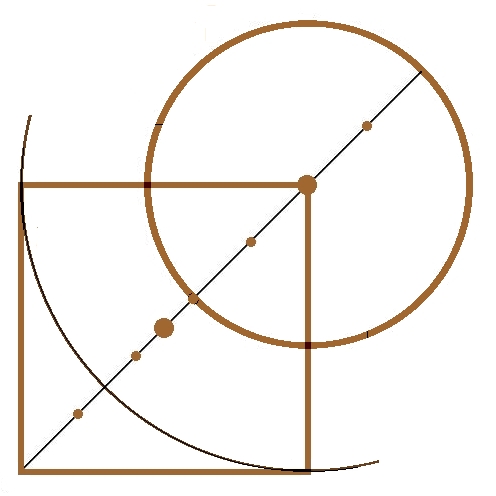 |
Las señas de los ángulos rectos que forma la serpiente
en su cuello y en su parte central, los extremos del pie de la figura humana
y la dirección que indica la barba, determinan la configuración de un
cuadrado; y, el falo muestra la dirección de la diagonal de esa figura
geométrica. Con la misma escala del triángulo y asociado a él, el cuadrado
tiene una superficie de 12,5 y su diagonal mide 5.
La prolongación de la hipotenusa cruza a la de la
alineación definida por el extremo del falo, la punta de la nariz y el dorso
de la mano. La distancia entre esa intersección y la de la hipotenusa y el
cateto con valor 4, es el radio de un círculo con superficie 12,56...
El
conjunto de cuadrado y círculo es una solución sencilla de la ‘cuadratura
del círculo’, pero con una discrepancia del 0,5%. Probablemente sería la más antigua conocida
y demostrada, según
el planteamiento:
A partir de un círculo construir un cuadrado que
tenga la misma superficie, solo con el empleo de un compás y una regla sin
graduar.
|
PROPORCIONES
Solución A
La intersección de la
diagonal del cuadrado con la hipotenusa marca el centro de un círculo que tiene
como radio la distancia a los extremos de la cabeza y del pie de la figura
humana. Asumiendo el giro de ésta para poner su eje paralelo al cateto con valor
4, considerando que es propio del hombre tener su altura equivalente a
F2 su ombligo señala la sección áurea con la división de 1 y
F, alineado con el
punto inferior de la basa del falo.
Siendo el diámetro del
círculo equivalente a F2,
éste más la unidad añadida al cateto con valor 4, hasta el extremo del brazo
extendido, determina el valor proporcional de
p. Los valores de
p y de
F pueden
ser como los que ahora se conoce, dependiendo del trazado y tamaño de las
figuras geométricas; sin embargo, el análisis trigonométrico establece un margen
de discrepancia del 1 por mil; para dar 3,14 en vez de 3,1415 en el caso de
p y de
1,62 en vez de 1,618 en el caso de
F.
Solución B
Con el mismo diseño
empleado en la lectura para encontrar la Solución A, se consigue el círculo.
Igualmente, se hace girar la figura humana hasta su posición vertical, pero con
una estatura menor, teniendo como límites la parte superior del círculo y la
base del cuadrado; obviamente esa altura es equivalente a
F2
, al ser la proporción del hombre; sin embargo, no hay una señal
para ubicar
F
en el ombligo en relación con alguna señal en la figura humana.
Con centro en el
vértice formado por la hipotenusa y el cateto con valor 4, y con un radio con
valor 1 señalado por el brazo extendido en la dirección de ese cateto, se traza
un arco circular hasta interceptar la prolongación de la hipotenusa, lográndose
en la dirección vertical una dimensión de 0,8 que añadida a la del mismo cateto
da 4,8 para, proporcionalmente, mostrar el valor de
p.
Por la solución
trigonométrica, o por la congruencia de triángulos, se determina que si la
altura del hombre es 4 y se la iguala a
F2,
la longitud total de 4,8 equivale a un
p de
3,1416...,
con una diferencia menor a 4 en cien mil del valor conocido ahora. Este
resultado podría mostrar que en esa cultura se conociese la razón entre 4,8 y
4
(igual a 1,2), como se empleó en otras culturas y épocas, para relacionar a
p con
F, por
medio de
F2
que es el paradigma de la proporción
humana.
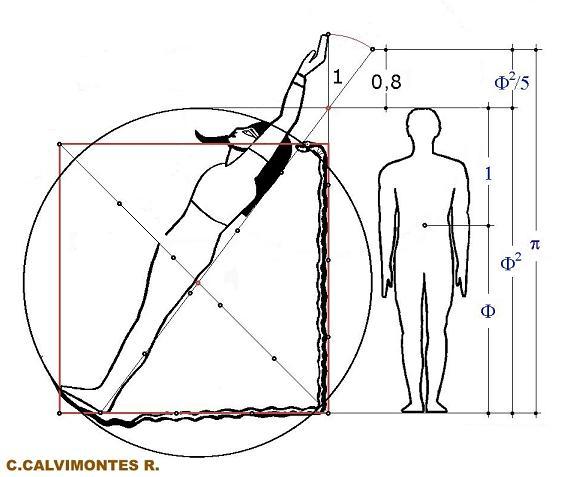
APORTE DE S. DE LUBICZ
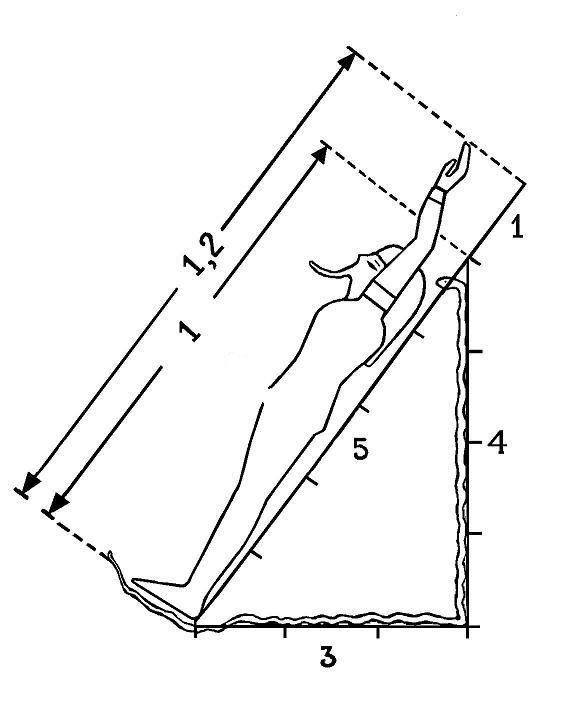
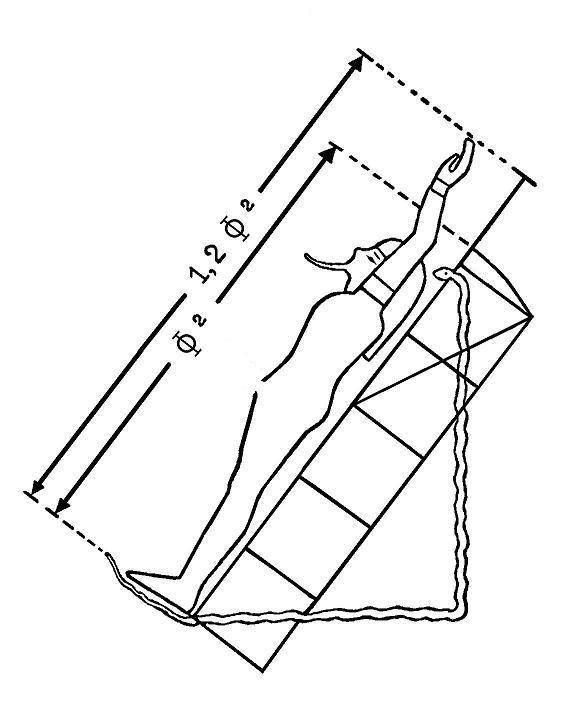 |
En el libro Secretos de la Gran Pirámide (Peter
Tompkins, México, 1989), se menciona el descubrimiento realizado por R. A.
Schwaller de Lubicz del triángulo 3-4-5 y de los valores de
p
y
F
en el dibujo que se halla en la tumba de Ramsés IX. Él habría establecido
que el falo divide al cuerpo en 1 y
F,
dando un total de
F2.
La longitud de la hipotenusa, 5 ó 1, es
mayor que la estatura de la figura humana representada, aunque, la altura
total de ésta con el brazo levantado sea de 6 ó 1,2. Sin
embargo, aunque la razón entre
p
y
F2
es aproximadamente 1,2 no corresponde a las proporciones señaladas en
el segundo dibujo. Además, según las proporciones antropométricas, es
imposible que el falo divida a la figura humana en 1 y
F.
Es decir, el
primer dibujo sólo expresa la relación de la longitud de la hipotenusa con
la altura señalada por el brazo levantado por el personaje (5 y 6,
ó 1 y 1,2), sin tomar en cuenta la altura del hombre. El
segundo dibujo muestra
F2,
equiparando Ö5+3
con un valor de 1; y, la longitud que se muestra como 1,2
F2
equiparada con Ö5+4
tiene un valor proporcional de 3,118... que está lejos de ser el de
p.
A pesar de esos errores, se reconoce que Schwaller de
Lubicz encontró el triángulo 3-4-5 e intuyó la presencia de
p
y de
F. |
Libros del autor:


IR A LA PÁGINA PRINCIPAL
http://urbtecto.es.tl