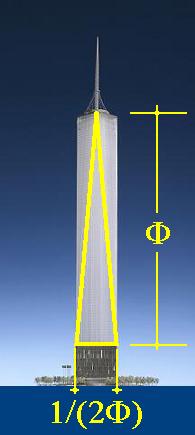
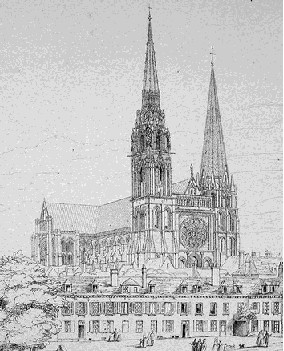EL TRIÁNGULO DORADO
CARLOS CALVIMONTES ROJAS
El autor reencontró la figura geométrica emblemática de las cualidades del Número de Oro, el Triángulo Dorado, definió sus propiedades y descubrió sus
manifestaciones en la Naturaleza y en la creación humana. En la portada del castillo l'Herm halló el mejor ejemplo de la aplicación de ese polígono, que habría sido conocido en la antigüedad de
diversas culturas y utilizado en forma expresa especialmente en el proporcionamiento armónico de obras arquitectónicas notables (Puerta del Sol de Tiwanaku y catedral de Milán). En otras, no menos
importantes, aparece por el empleo de criterios heredados de composición general (templos de México), se revela espontáneamente por el diseño con excelencia estética y/o estructural (proyecto de
Norman Foster en Moscú y Torre Eiffel) o se manifiesta por emulación de proporciones existentes en la Naturaleza (templo de la Sagrada Familia de Antoni Gaudí con torres que imitan formas de
gasterópodos).
Aquí se expone la configuración del Triángulo Dorado, su presencia en la Naturaleza y su expresión en la arquitectura como canon de diseño, calculado o
intuitivo, especialmente en la configuración de formas externas; con las excepciones de la catedral de Milán, donde participa en el diseño interno, y de la Puerta del Sol de Tiwanaku, donde el
Triángulo Dorado es un componente más de su composición.
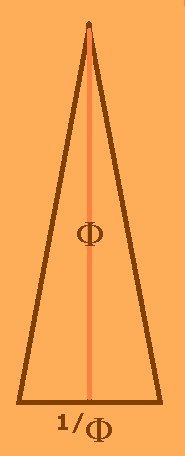 |
CONFIGURACIÓN
El Triángulo
Dorado
es el que reúne el conjunto de cualidades esenciales del Número de Oro: él mismo, su inverso y su cuadrado; y, además, no se deriva de ninguna
otra figura geométrica.
Tiene de altura
F
(
1,618033989...
) y de base 1/
F
(
0,618033989...
)
.
La razón entre la altura del Triángulo y su base es
F
2
(2,618033989...).
Si la base se iguala a 1 la altura es
F
2
Por lo tanto, se trata del Triángulo Dorado por excelencia, figura geométrica paradigmática por sus armónicas proporciones. |
|
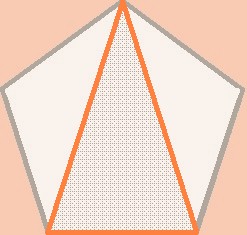
Se conoce generalmente como ‘triángulo dorado’ a uno isósceles cuyos lados iguales valen
F
2 y su base
F
; sin embargo, esta figura es un producto de la configuración del pentágono que, como es sabido, está absolutamente definido por
F
en todas sus partes y figuras derivadas. Ese ‘triángulo dorado’ tiene como lados iguales a dos de las diagonales del pentágono y su base es un lado de éste. |
|
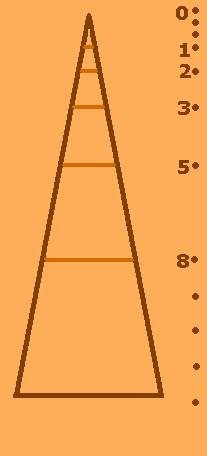
El Triángulo Dorado es parecido a la figura que se puede construir con la Serie de Fibonacci (0-1-1-2-3-5-8-13-21.......). Ver NOTAS al final.

Castillo de l'Herm de Jean III de Calvimont (s. XV)
 |
De esa obra del gótico flamígero se conoce como 'tesoro' al conjunto de elementos en el que se destacan, como joyas arquitectónicas, la portada, la escalera
en caracol y la bóveda con una nervadura triangulada, que se configuran con el Número de Oro.
Entre notables obras de arquitectura de diferentes épocas y lugares con las proporciones del Triángulo Dorado, se destaca la bella composición de la portada
de ese castillo por su detallado diseño con la participación del Número de Oro. |
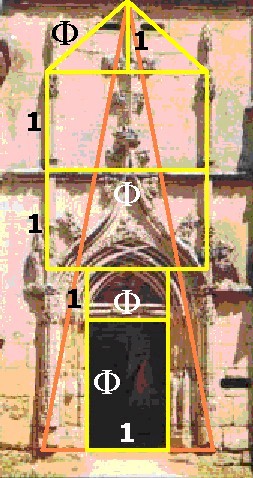 |
PRESENCIA DEL TRIÁNGULO DORADO
Como ocurre con toda manifestación singular de
F
, el Triángulo Dorado está presente en la Naturaleza y en la creación humana, especialmente en obras de arquitectura; tal como está definido en su configuración o
con su mitad longitudinal [con base 1/(2
F
)]. En las ilustraciones del primer caso se muestra el eje de simetría bilateral.

Hoja de Arce Japonés,
acer palmatum |

Hoja del Árbol de Estoraque,
liquidambar styraciflua |

Ciprés de Lawson, chamaecyparis lawsoniana
Abeto rojo, picea abis
Sugi, cryptomeria japonica |

Puya Raimondi
pourretia gigantea |
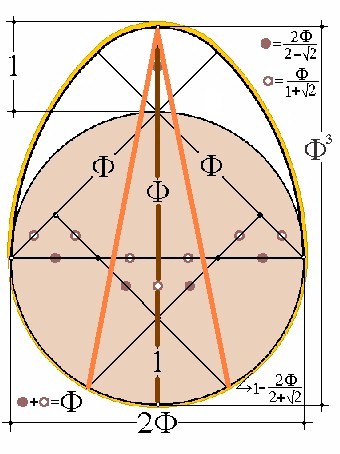
Configuración del huevo de gallina según C. Calvimontes R.
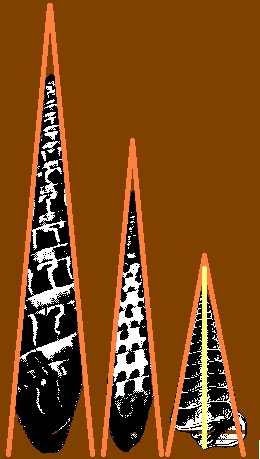
Gasterópodos
Superposición a gráficos del libro The Curves of Life de Theodore Andrea Cook |

Globigerina
Superposición a dibujo de Ernst Haeckel |
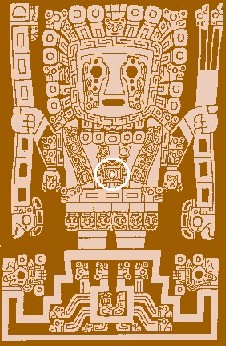
Figura central en la Puerta del Sol de Tiwanaku. Se destaca su ombligo, vértice común de los triángulos de composición con el Número de Oro. |
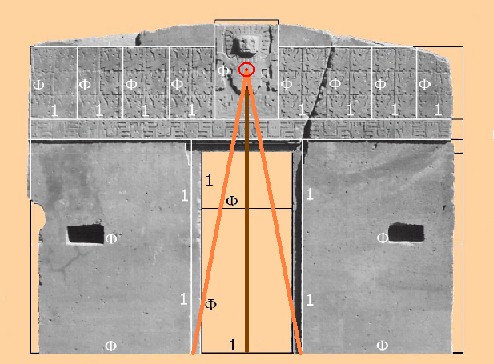
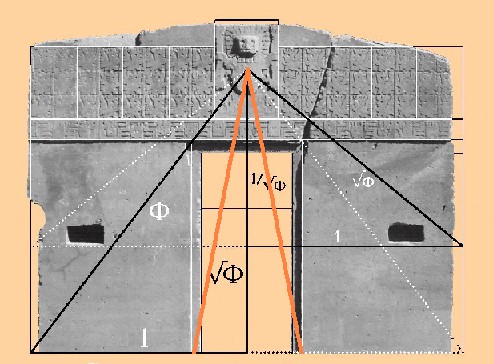
|
Configuración de la Puerta del Sol de Tiwanaku (circa s. V)
según C. Calvimontes R.
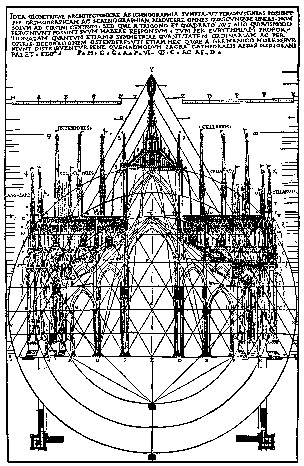
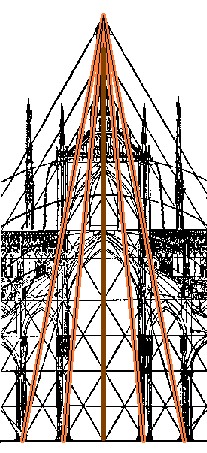
Catedral de Chartres (s. XIII)
Catedral de Colonia (s. XIV)

Catedral de Milán (s. XIV)
Armonización de las proporciones de la catedral de Milán por el arquitecto Stornalocho en 1391 con el empleo de triángulos y dada a conocer, con el añadido de
círculos, por Cesare Cesariano en 1591 en su traducción y comentario de la obra de Vitruvio. En 1931 Ernst Moessel utilizó esa base para proponer una tesis que interpreta el diseño de Stornalocho.
Sin embargo, el trabajo de Moessel sólo considera los triángulos equiláteros externos y no los dos triángulos isósceles interiores. Precisamente el mayor de éstos es un Triángulo Dorado
completo y el interior su mitad. Se presenta sin ninguna intervención el diseño difundido por Cesariano y en la copia de su parte central se destaca la presencia de esas dos figuras triangulares.
Castillo del Bran (s. XIV), donde vivió Vlad II, conocido como conde Drácula
Portadas de templos en la ciudad de México (circa s. XVI).
Superposición a dibujos de Domingo García Ramos
Torre Eiffel (s. XIX). Superposición a dibujo de Gustave Eiffel

Fuente del Cólera de Gottfried Semper, Dresde (s. XIX)
Dibujo de C. Calvimontes R.
Templo de la Sagrada Familia (s. XX) de Antoni Gaudí
Proyecto de Norman Foster
Edificio de 600 m de altura en el centro internacional Moscow City (s. XXI)
Proyecto de Daniel Libeskind y David Childs
Edificio Freedom
Tower, de 541 m, en la Zona Cero de Nueva York (s. XXI)
Proyecto de Adrian Smith
Edificio Burj Dubai, de 808 m, en Dubai (s.
XXI)
NOTAS
DISCREPANCIA CON LA SERIE DE FIBONACCI
Si se construye con los términos de la Serie de Fibonacci (0-1-1-2-3-5-8-13-21.......) una figura que vaya teniendo como altura la suma de los términos
de la misma y como bases sucesivas las longitudes determinadas por esos mismos términos, a partir de aproximadamente el quinto término de la indicada Serie (3) esa figura adopta los lados de
una extendida curva cóncava que tiene como asíntotas los lados del Triángulo Dorado.
En consecuencia, se observa el parecido entre el Triángulo Dorado y el desarrollo gráfico de esa Serie sólo a partir de quinto término de la misma
(0-1-1-2-
3
-5-8-13-21.......). El Triángulo Dorado es más parecido a la figura construida con la serie 0...(un valor de 8 distribuido entre 0 y
3)...3-5-8-13-21........
Se hace notar que en la figura construida con los valores de la Serie de Fibonacci la longitud horizontal correspondiente a cada término de la misma, a
partir del 3 es menor que la base que en ese punto tendría el Triángulo Dorado, diferencia que se puede apreciar mejor con una graficación a gran escala, y que va disminuyendo en la medida en que
avanza el desarrollo de dicha Serie.
COMPROBACIÓN DEL AJUSTE PAULATINO
Se puede verificar que se da un ajuste entre el Triángulo Dorado y la figura construida con los valores de la Serie de Fibonacci cuando el desarrollo de
ésta ha alcanzado un término que permite conseguir un aceptable
F
(1,618033989...), dividiendo ese término por su anterior.
Por ejemplo, con el término 30 de esa Serie se cumple la condición señalada y se alcanza la cifra 514.229 que es, en ese lugar, la base de su
triángulo. Asimismo, la suma de todos los términos de ese desarrollo, 1.346.268, es su altura. Al dividir ésta entre la base se obtiene 2,61803... que, con 5 decimales, se aproxima a
F
2
COMPARACIÓN ENTRE LAS SERIES
Con la serie 0...(8)...3-5-8-13-21....... se puede construir una figura (sus lados no son líneas rectas) que es más parecida a la del Triángulo Dorado;
pero, desde su inicio, esa serie es mayor en una unidad a la Serie de Fibonacci, aunque la consecuencia de dicha diferencia parece insignificante, sobre todo a la larga;
por ejemplo, a la altura del término 31 de ella se obtiene un
F
menor en casi 2 millonésimas a la que resulta a la altura del término 30 de la Serie de Fibonacci. Sin embargo, recién el término 37 de la primera
iguala al 30 de la segunda en la obtención del mismo valor de
F
IR AL
ÍNDICE
http://urbtecto.es.tl