AUTHOR Gudea, 'the chosen one', is the paradigmatic character of the Sumer Renaissance. Ensi o Patesi, was at the same time prince, ruler, and priest of the city-state of Lagash (he governed between 2144 - 2124 or 2122 a.) At the time of the greatest splendor of the ancient Mesopotamian civilization. Lagash is the current Tello or Al Hiba, on the banks of the Tigris River, 300 km southeast of Baghdad in Iraq. Of him and his work has been commented extensively, it has even been said that he was a god. He was the most portrayed man of antiquity and of the many sculptures that were made the best known is the seated person who has been called 'the Architect of the Plane' and which is preserved in the Louvre Museum. In one of the commemorative documents that he wrote he states that he invented "a new way of building, not used before by any sovereign". It has been assumed so far that it referred to a new type of brick, but it is more likely that it alluded to a useful geometric resource. This, attending to a problem of all times, makes it easy to put 'square' the rethinking of design in the field, a construction site or task of surveying, in cases of the different ratio between the lengths of the legs of triangles rectangles with sides of whole numbers.

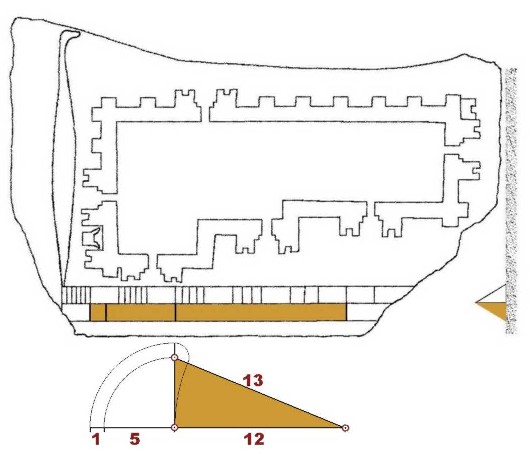
SUPPORT On the knees of the Architect of the Plane, there is a drawing board, in which the plan of a supposed fortified temple is engraved, accompanied by a drawing instrument and another measuring instrument. This has the same shape and size as the one currently used for technical drawing and is known as a scaler. In the inner band of the instrument, there is a measuring rule with sexagesimal basis. In the outer strip, there are marks that indicate successively magnitudes proportional to 1, 5 and 12, which make a total of 18 between the extremes. The necessary and meticulous measurements were made on the sculpture.

PURPOSE

The dimensions found in the outer band of the instrument show the quantitative characteristics of the right triangle with sides 5, 12 and 13: the difference between the major leg and the hypotenuse, 1, the minor leg that is odd, 5, the long leg, 12, and the sum of the minor leg and the hypotenuse, 18. The disposition of the measures in the rule allows us to infer that we deliberately wanted to show the linear development of that triangle and suggest the procedure for the design of this and similar ones. The set of these characteristics defines, generalizing, what can be called Gudea Triangles: being rectangles, their sides are measured with integers, and their solution does not require the use of square roots.

GUDEA THEOREM

 For the verifiable merit of the proposed geometric solution

PROPOSITION

In right triangles whose sides are measured with integers if: the hypotenuse is odd, one leg is odd with the other pair and the difference between the largest and the hypotenuse is 1 or 2; the value of the hypotenuse is equal to the major leg plus 2 if the minor leg is even and 1 if it is odd.

DEMONSTRATION Y REPERTOIRE

AXIOMATIC CONDITIONS

• The hypotenuse is always odd (E).

• If one leg is even, the other is odd (A and B).

• The difference between the major leg and the hypotenuse can only be 1 or 2 (C).

COROLLARIES

• The minor cathetus (A) is a submultiple of the sum (G) of the major cathetus (B) and the hypotenuse (E).

• The sum (F) of the major cathetus (B), the two catheti (A + B) and the difference between the major cathetus and the hypotenuse (C), is always an even number.

• If the sum (D) of the catheti (A + B) plus the difference between the major cathetus and the hypotenuse (C) is an odd or even number, the same thing happens with the major cathetus. (B).

• If the sum (G) of the major cathetus (B) and the hypotenuse (E) is an even or odd number, the same applies to the minor cathetus (A).

________________________________________________________

1. In a drawing found in the tomb of Ramses IX, the pharaoh who lived ten centuries after Gudea, a similar solution was described in a right triangle 3-4-5, with an additional 1 in a prolongation of the major leg. Six centuries later Pythagoras (who nurtured knowledge in Mesopotamia and Egypt) became famous for demonstrating the quadratic relations between the sides of right triangles. See Geometry in ancient Egypt.

2. It should take 16 long centuries for the Samos School to be expressed in several mathematical discoveries the Pythagorean Theorem: in a right triangle "the sum of the squares of the legs equals the square of the hypotenuse" in a singular demonstration of what the mathematicians of Babylon and India were doing in the configuration of right triangles.

3. The discovery of Gudea's Theorem was made in 1991 after the measurements made by the author in the sculpture of the Architect of the Plane in the Oriental Arts Room of the Louvre Museum, and has the record of intellectual property in favor of its author and owner Carlos Calvimontes Rojas, with the title "Theorem for the solution of right triangles without the use of square roots", in the Copyright Directorate of the Ministry of Economic Development of Bolivia, with Administrative Resolution No. 1-1001-386 / 2001 on May 29, 2001 in the city of La Paz.

4. The web page “Mathematical mystery of ancient clay tablet solved” states that “UNSW scientists have discovered the purpose of a famous 3700-year-old Babylonian clay tablet, revealing it is the world’s oldest and most accurate trigonometric table.” Noting that it was “…possibly used by ancient mathematical scribes to calculate how to construct palaces and temples and build canals.” And that knowledge “…reveals an ancient mathematical sophistication that had been hidden until now.” See also: “Mathematical secrets of ancient tablet unlocked after nearly a century of study” and “The Babylonian tablet Plimpton 322”

5. The Plimpton 322 tablet - by the number of the George Arthur Plimpton collection - was found in the early 1900s in Larsa (Tell Senkereh), Iraq. It was dated between 1820 and 1762 a. C., that is to say after three centuries of which Gudea instructed to engrave in the sculpture with his effigy the key of the solution of the triangles rectangles with whole numbers.

GO TO INDEX

urbtecto@gmail.com