Solución de los Triángulos Rectángulos según el Teorema de Gudea

CARLOS CALVIMONTES R.

Desde la remota antigüedad en la cultura sumeria de Mesopotamia fue conocida la configuración básica de triángulos rectángulos con números enteros para resolver problemas prácticos de la construcción y la agrimensura, esa aplicación fue transmitida a culturas posteriores1 y ha llegado hasta la actualidad en la práctica cotidiana de la construcción para poner a escuadra los elementos de una obra. Al haber sido reconocida la importante trascendencia de esa configuración2, hace 41 siglos se dejó el testimonio de cómo se resolvía la relación entre los lados de esos triángulos rectángulos en una forma simple y elegante, descrita en la evidencia que encontré en 1991 en la famosa escultura del más antiguo arquitecto del que se tiene noticia, y que denominé el Teorema de Gudea3 en justo reconocimiento al creador del algoritmo por el cual se puede deducir la dimensión de uno de los lados de un triángulo rectángulo si se conoce las medidas de los otros lados que sean números enteros.

26 años después de mi descubrimiento científicos de la Universidad de Nueva Gales del Sur a mediados del 2017 dieron la noticia4  que habían encontrado tripletes de triángulos rectángulos en la tablilla Plimpton 3225 pero no llegaron a señalar que esos tripletes son el resultado de una fórmula admirable cuyo conocimiento he difundido en diversos medios.

ESCULTURA DEL ARQUITECTO DEL PLANO
AUTOR

Gudea, ‘el elegido’, es el personaje paradigmático del Renacimiento de Sumer. Ensi o Patesi, fue al mismo tiempo príncipe, mandatario y sacerdote de la ciudad-estado de Lagash (gobernó entre 2144 - 2124 ó 2122 a. C.) en la época del mayor esplendor de la antigua civilización mesopotámica. Lagash es la actual Tello o Al Hiba, a orillas del Río Tigris, a 300 Km. al sudeste de Bagdad en Irak.

De él y de su obra se ha comentado extensamente, incluso se ha dicho que era un dios. Fue el hombre más retratado de la antigüedad y de las muchas esculturas que se le hicieron la más conocida es la sedente que se ha llamado 'el Arquitecto del Plano' y que se conserva en el Museo del Louvre.

En uno de los documentos conmemorativos que él escribió manifiesta que inventó “una nueva manera de construir, no empleada antes por ningún soberano”. Se ha supuesto hasta ahora que se refería a un nuevo tipo de ladrillo, pero es más probable que aludía a un útil recurso geométrico. Éste, atendiendo a un problema de todos los tiempos, facilita poner ‘a escuadra’ el replanteo de un diseño en el terreno, de una obra de construcción o tarea de agrimensura, en casos de diferente razón entre las longitudes de los catetos de triángulos rectángulos con lados de números enteros.

TABLERO EN EL 'ARQUITECTO DEL PLANO'
SOPORTE

Sobre las rodillas del Arquitecto del Plano se encuentra un tablero de dibujo, en el cual está grabado el plano de un supuesto templo fortificado, acompañado por un instrumento de dibujo y otro de medida. Éste tiene igual forma y tamaño que el empleado actualmente para el dibujo técnico y que se conoce como escalímetro. En la franja interior del instrumento hay una regla de medición con base sexagesimal. En la franja exterior existen marcas que señalan en forma sucesiva magnitudes proporcionales a 1, 5 y 12, que hacen un total de 18 entre los extremos. Las necesarias y minuciosas mediciones fueron realizadas sobre la escultura.
PROPÓSITO

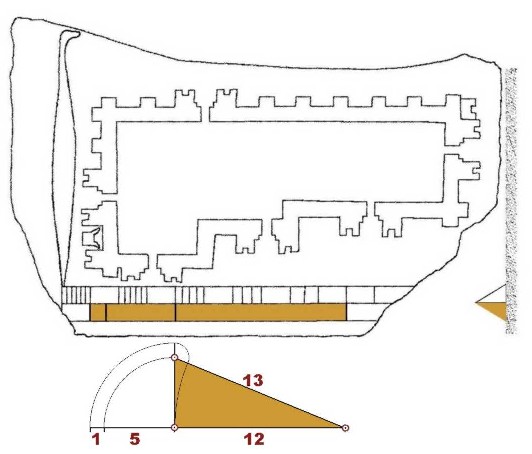
Las dimensiones encontradas en la franja exterior del instrumento muestran las características cuantitativas del triángulo rectángulo con lados 5, 12 y 13: la diferencia entre el cateto mayor y la hipotenusa, 1, el cateto menor que es impar, 5, el cateto mayor, 12, y la suma del cateto menor y la hipotenusa, 18. La disposición de las medidas en la regla permite inferir que se quiso deliberadamente mostrar el desarrollo lineal de ese triángulo y sugerir el procedimiento para el diseño de éste y de otros semejantes. El conjunto de esas características define, generalizando, a los que se puede denominar como Triángulos de Gudea: siendo rectángulos, sus lados se miden con números enteros y su solución no requiere el empleo de raíces cuadradas.

REGLA GRADUADA CON SOLUCIÓN DEL TRIÁNGULO RECTÁNGULO

TEOREMA DE GUDEA

 Por el mérito verificable de la solución geométrica planteada

PROPOSICIÓN

En los triángulos rectángulos cuyos lados se miden con números enteros si: la hipotenusa es impar, un cateto es impar siendo el otro par y la diferencia entre el mayor y la hipotenusa es de 1 ó 2; el valor de la hipotenusa es igual al cateto mayor más 2 si el cateto menor es par y más 1 si es impar.

DEMOSTRACIÓN Y REPERTORIO

CATETO MENOR

CATETO MAYOR

E-B

A + B + C

HIPOTENUSA 

D – A  ó  B + C

B + D

B + E

A

B

C

D

E

F

G

3

4

1

8

5

12

9

5

12

1

18

13

30

25

7

24

1

32

25

56

49

8

15

2

25

17

40

32

9

40

1

50

41

90

81

12

35

2

49

37

84

72

16

63

2

81

65

144

128

CONDICIONES AXIOMÁTICAS

COROLARIOS

________________________________________________________

1. En un dibujo que se encuentra en la tumba de Ramsés IX, faraón que vivió diez siglos después de Gudea, se describió una solución semejante en un triángulo rectángulo 3-4-5, con un 1 adicional en una prolongación del cateto mayor. Seis siglos más tarde Pitágoras (que se nutrió de conocimientos en Mesopotamia y Egipto) se hizo famoso por la demostración de las relaciones cuadráticas entre los lados de los triángulos rectángulos. Ver Geometría en el antiguo Egipto.

2. Debían pasar 16 largos siglos desde para que en la Escuela de Samos dentro de varios descubrimientos matemáticos se expresara el Teorema de Pitágoras: en un triángulo rectángulo "la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa" en una demostración singular de lo que manejaban los matemáticos de Babilonia y la India en la configuración de los triángulos rectángulos. 

3. El descubrimiento del Teorema de Gudea fue hecho el año 1991 después de las mediciones realizadas por el autor en la escultura del Arquitecto del Plano en la Sala de Artes Orientales del Museo del Louvre y tiene el registro de la propiedad intelectual en favor de su autor y tilular Carlos Calvimontes Rojas, con el título "Teorema para la solución de triángulos rectángulos sin el empleo de raíces cuadradas", en la Dirección de Derecho de Autor del Ministerio de Desarrollo Económico de Bolivia, con la Resolución Administrativa Nº 1-1001-386/2001 con fecha 29 de mayo del 2001 en la ciudad de La Paz.

4. En la página web Mathematical mistery of ancient clay tablet solved se enuncia que “Científicos de la UNSW descubrieron el uso de una tablilla de arcilla babilónica de 3700 años de antigüedad, que revelando que es la tabla trigonométrica más antigua y más precisa del mundo.” Señalando que fue “…posiblemente utilizada por antiguos escribas matemáticos para calcular cómo edificar palacios y templos y construir canales.” Y que ese conocimiento “…revela una antigua sofisticación matemática que hasta ahora se había ocultado.” Ver también: Mathematical secrets of ancient tablet unlocked after nearly a s¡century study y The Babylonian tablet Plimpton 322

5. La tablilla Plimpton 322 —por el número de la colección de George Arthur Plimpton— fue encontrada a principios de 1900 en Larsa (Tell Senkereh), Irak. Fue fechada entre 1820 y 1762 a. C., o sea después de tres siglos de que Gudea instruyó grabar en la escultura con su efigie la clave de la solución de los triángulos rectángulos con números enteros.

Aunque se trate del testimonio escrito más antiguo que se conozca es indudable que pueden existir otras tablillas con información semejante o referente entre las del medio millón encontradas o en otras aún no descubiertas. Además, 26 años antes del estudio de los científicos de la Universidad de Nueva Gales del Sur —en otro medio y en forma gráfica grabada tres siglos antes de la Plimpton 322—, se halló el testimonio incuestionable del procedimiento para conocer la relación de los lados de triángulos rectángulos con números enteros en la escultura del Arquitecto del Plano. Ese descubrimiento y su interpretación son totalmente verificables.

 

 

IR AL ÍNDICE

http://urbtecto.es.tll

1 urbtecto@gmail.com